Out of Kilter Flow Algorithm and its applications in Supply Chain

Out of Kilter Flow Algorithm and its applications in Supply Chain

One of the finest mathematician born in 20th Century D. R. Fulkerson is popular for his excellent work on solving maximal flow problems which is co-developed with L. R. Ford Jr. Their work is famous as Ford-Fulkerson algorithm. However, Fulkerson also published a paper in 1961 entailing a minimum cost flow algorithm known as Out-of-Kilter flow algorithm.

Although, many minimum cost flow algorithm were introduced since then, the unique structure of OKF makes it still very relevant and useful because of its ability to exploit underlying network structure. Readers familiar with operations research area would know the computational advantage of network flow models over more general mathematical programming models. OKF is used for solving many network problems those include below but are not limited to,

1. Transportation Problem

2. Assignment Problem

3. Shortest Path problem

4. Maximum flow problem

5. Minimum-cost-flow problem

6. Transshipment problem

OKF is a very general purpose algorithm and easy to understand. Example of practical implementation for this algorithm are “An interdiction model of Highway Transportation” and “A Model for Estimating military personnel Rotation based requirements”.

Problem definition of OKF is to find a flow, Xij that satisfies flow constraints and conservation of flow equations and minimize the total cost. This can be represented as below,

Objective Function:

minimize ∑CijXij Cij is cost of sending flow Xij from node i to node j

ij

Constraints:

Lij ≤ Xij≤ Uij Lij and Uij are lower and upper limit of flow permissible through link ij

Flow Conservation:

∑Xji - ∑Xij = 0 for all i

j j

Let ∏i denote the price a consumer at node I must pay for a unit of a commodity. The ∏I will be related to the amount demanded at some nodes, since as the amount demanded increases, the overall difficulty in supplying it will increase. So a net arc cost can be defined as

Cij = Cij + ∏I - ∏j

The new cost Cij, represents the total cost of the system, consumer and distributor – of transporting one unit for flow from node I to node j.

Basically, this method compares the cost of retaining a unit at node i with the cost of moving it to node j. In Moving a unit of flow from I to j, the commodity price at i, ∏I, is foregone, and an actual transportation cost, Cij, is incurred. If the sum of these costs is greater than commodity price at j, ∏j, then it does not pay to ship a unit from I to j. The Cij will be positive. On the other hand, if a unit at j costs more than at I plus the transportation cost, Cij will be negative, the system benefits from the move and shipment from I to j is profitable. Obviously we are indifferent when the system cost at i and transportation cost is balanced means zero.

The above explaination yeailds following conditions:

1. If Cij < 0 then Xij = Uij

2. If Cij = 0 then Lij ≤ Xij≤ Uij

3. If Cij > 0 then Xij = Lij

An arc that meets above optimality condition is call “in-Kilter” and that which do not satisfy these conditions are called “out-of-Kilter”

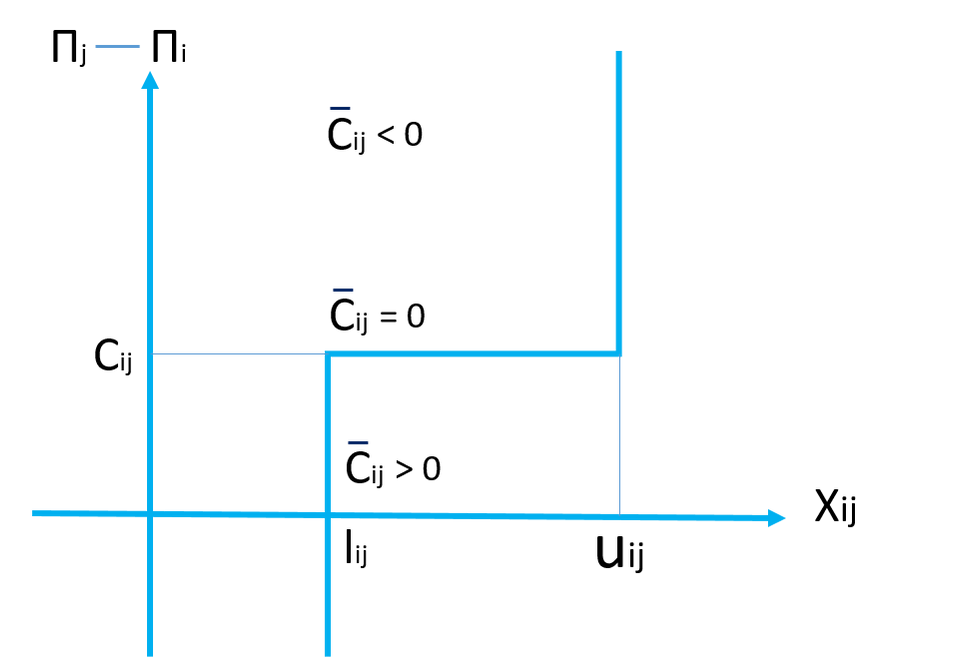
A Kilter number is associated with each arc and feasibility is checked. The attempt is made to reduce the kilter number and try to bring the arc in-kilter while not violating the constraints.

Straight forward application for this can be capacitated transportation problem, determining maximum flow in a capitated network and finding the shortest route through a network in which costs on arcs are times or distances.

Milk-Run Consulting

https://milk-run.co.in