Seven Bridges of Konigsberg

In the early 1730’s, mathematician Leonhard Euler was tasked to solve a strange problem. The city of Königsberg in Prussia (now Kaliningrad, Russia) was set on both sides of the Pregel River, and included two large islands which were connected to each other, or to the two mainland portions of the city, by seven bridges. The problem was to devise a walk through the city that would cross each of those bridges once and only once.

By way of specifying the logical task unambiguously, solutions involving either

1. reaching an island or mainland bank other than via one of the bridges, or

2. accessing any bridge without crossing to its other end

were explicitly unacceptable.

Actual layout of the seven bridges, highlighting the river Pregel and the bridges (source: Wikipedia)

Euler responded negatively for any solution to this problem but his analysis paved path for modern way of exploring Graph theory and formed basis for that.

The above graph can be simplified to below (source: mathisfun.com)

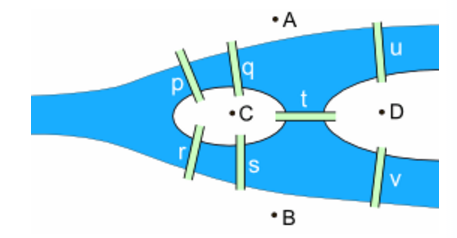
A,B,C,D are the four areas of the town and one should cross each of the bridge p,q,r,s,t,u and v exactly once. The diagram can be further simplifies as below

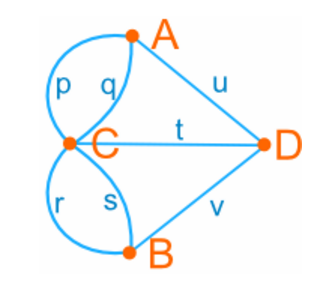
Readers can try drawing each line p, q, r, s, t, u and v only once, without removing your pencil from the paper (you may start at any point).

In Simple terms, one replaces each land mass with an abstract "vertex" or node, and each bridge with an abstract connection, an "edge", which only serves to record which pair of vertices (land masses) is connected by that bridge. The resulting mathematical structure is called a “graph”.

If you look at the graph above carefully, you will notice that all vertices (land mass) are having odd number of edges or links connected to them. Euler observed that in-order for someone to go through each of bridge exactly once, corresponding land mass should have even number of bridges connected to it which is a contradiction in above graph.

In modern mathematical terms, Euler proposed that that the possibility of a walk through a graph, traversing each edge exactly once, depends on the degrees of the nodes. The degree of a node is the number of edges touching it. Euler's argument shows that a necessary condition for the walk of the desired form is that the graph be connected and have exactly zero or two nodes of odd degree. Such a walk is now called an “Eulerian path” or Euler walk in his honor. Further, if there are nodes of odd degree, then any Eulerian path will start at one of them and end at the other. Since the graph corresponding to historical Königsberg has four nodes of odd degree, it cannot have an “Eulerian path”.

Euler's work was presented to the St. Petersburg Academy on 26 August 1735, and published as Solutio problematis ad geometriam situs pertinentis (The solution of a problem relating to the geometry of position) in the journal Commentarii academiae scientiarum Petropolitanae in 1741. It is available in English in The World of Mathematics.

Milk-Run Consulting

https://milk-run.co.in